编译器优化那些事儿(4):归纳变量原创
0. 基础知识盘点
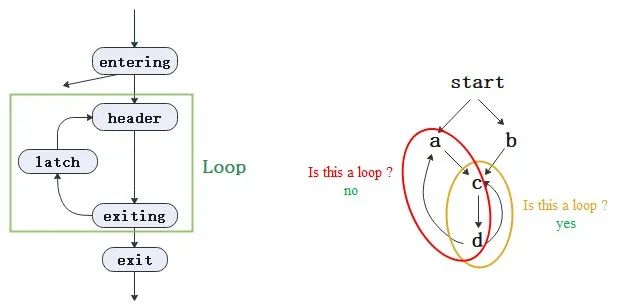
0.1 循环(loop)
定义
loop(llvm里理解为natural loop)是定义在CFG中的一个结点集合L,并具有以下属性[1][2]:
-
有单一的入口结点(称为header),该结点支配loop中的所有结点; -
存在一条进入循环头的回边;
相关术语
-
entering block:一个非loop内的结点有一条边连接到loop。当只有一个entering block且其只有一条边连接到header,称之为preheader;作为非loop结点的peheader支配整个loop; -
latch:有一条边连接到header; -
backedge:称为回边,一条从latch到header的边; -
exiting edge:一条边从loop内到loop外,边的出发结点称之为exiting block,目标结点称之为exit block;
上面右图中,***域是一个loop,而红**域不是,为什么呢?
因为红**域a和c都是入口结点,不满足单一入口结点的性质。
0.2 Scalar Evolution(SCEV)
定义
SCEV是编译器对变量进行分析的优化(往往只针对整数类型),且主要用于分析循环中变量是如何被更新的,然后根据这个信息来进行优化。
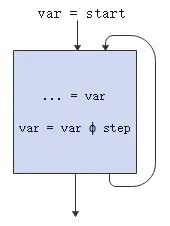
循环链
如图所示,循环中归纳变量var的起始值为start,迭代的方式为ϕ,步长为step;
它的循环链(chrec,Chains of Recurrences)如下:
var = {start, ϕ , step}
// ϕ∈{+,∗}
// start: starting value
// step: step in each iteration
举个例子:
int m = 0;
for (int i = 0; i < n; i++) {
m = m + n;
*res = m;
}
那么m的循环链为:m = {0,+,n}。
1. Induction Variable(归纳变量)
1.1 定义
循环的每次迭代中增加或减少固定量的变量,或者是另一个归纳变量的线性函数。
举个例子[3],下面循环中的i和j都是归纳变量:
for (i = 0; i < 10; ++i) {
j = 17 * i;
}
1.2 益处
归纳变量优化的好处,有但不局限于以下几点:
-
用更简单的指令替换原来的计算方式。
比如,上面的例子中识别到归纳变量,将对应的乘法替换为代价更小的加法。j = -17;
for (i = 0; i < 10; ++i) {
j = j + 17;
} -
减少归纳变量的数目,降低寄存器压力。
extern int sum;
int foo(int n) {
int i, j;
j = 5;
for (i = 0; i < n; ++i) {
j += 2;
sum += j;
}
return sum;
}当前的loop有两个归纳变量:i、j,用其中一个变量表达另外一个后,如下:
extern int sum;
int foo(int n) {
int i;
for (i = 0; i < n; ++i) {
sum += 5 + 2 * (i + 1);
}
return sum;
} -
归纳变量替换,使变量和循环索引之间的关系变得明确,便于其他优化分析(如依赖性分析)。举例如下,将c表示为循环索引相关的函数:
int c, i;
c = 10;
for (i = 0; i < 10; i++) {
c = c + 5; // c is incremented by 5 for each loop iteration
}转换为:
int c, i;
c = 10;
for (i = 0; i < 10; i++) {
c = 10 + 5 * (i + 1); // c is explicitly expressed as a function of loop index
}
2. 实践
2.1 相关编译选项
| compiler | option |
|---|---|
| gcc | -fivopt |
| 毕昇 | -indvars |
2.2 优化用例
归纳变量的优化(ivs)在llvm中的位置是:llvm\lib\Transforms\Scalar\IndVarSimplify.cpp
让我们通过一个用例,看看毕昇编译器的优化过程。
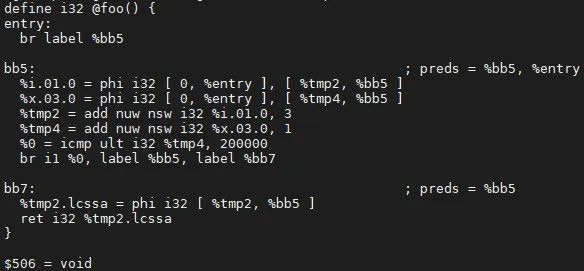
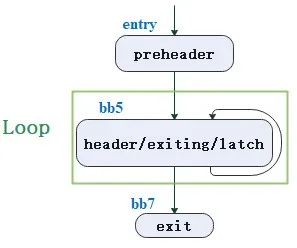
如下图,假设上面func里面的部分就是要优化的代码,下面func里面就是预期生成的结果:
它的IR用例test.ll是:
编译命令是:
opt test.ll -indvars -S
当前的例子中,header、latch和exiting block都是同一个BB,即bb5。
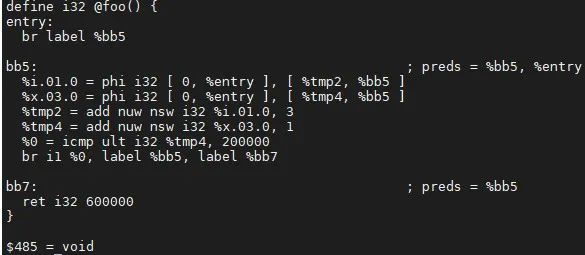
步骤一:依据 def-use 关系,遍历loop的 ExitBlock 中phi结点的操作数的来源,计算出最终值同时替换它,继而替换该phi结点的使用。
例子中,计算 %tmp2.lcssa ,其唯一的操作数是 %tmp2 = add nuw nsw i32 %i.01.0, 3 ,该表达式所在的loop是bb5,此时 %tmp2 的循环链为
%tmp2 = {3,+,3}<nuw><nsw><%bb5>
获取当前loop的不退出循环的最大值是199999,那当前 %tmp2=add(3, mul(3,199999))=600000;接下来会看当前的替换不是高代价(代价的计算会依据不同架构有所不同),同时在phi结点的 user 中替换该值。优化结果如下:
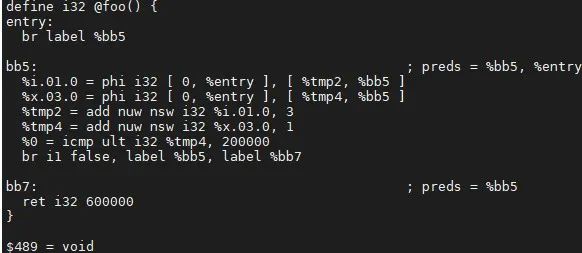
步骤二:遍历 ExitingBlock ,对其跳转条件进行计算,依据 def-use 的关系,删除相应的指令。
例子中,计算出 br i1 %0, label %bb5, label %bb7 的 %0 是 false,跳转指令替换后,%0 = icmp ult i32 %tmp4,200000 不存在 user,将其加入到“死指令”中。优化结果如下:
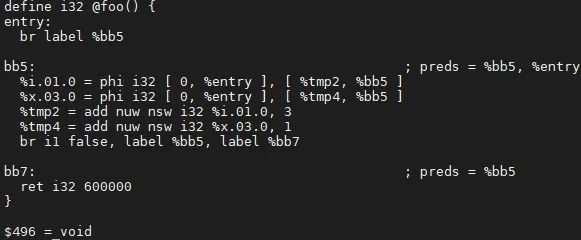
步骤三:删除所有“死指令”,并看看他的操作数是否要一并删除。
例子中,作为 %0 的操作数的 %tmp4 还有其他的 user %x.03.0,因此不能被视为“死指令”被删除。优化结果如下:
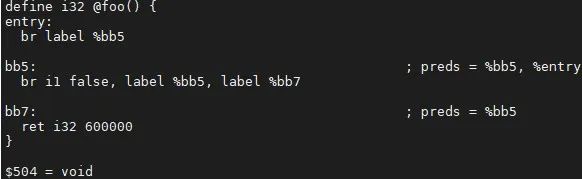
步骤四:删除 HeaderBlock 中的“死”phi结点。
例子中, %tmp4 和phi结点 %x.03.0 构成了一个不会有成果的循环,就会删除它们,同理删除 %tmp2 和 %i.01.0 。优化结果如下:
参考
[1] https://llvm.org/docs/LoopTerminology.html
[2] 《编译原理》 [美]Alfred V.Aho,[美]Monica S.Lam,[美]Ravi Sethi等著,赵建华,郑滔等译
[3] https://en.wikipedia.org/wiki/Induction_variable