關於用 Go 实现堆和堆操作,可能是最通俗易懂的讲解了原创
堆是一种树形数据结构,分为大顶堆和小顶堆,顾名思义,大顶堆就是堆顶(第一个元素)始终存放的是这组元素中的最大元素,小顶堆就是堆顶元素是最小元素。如果需要从一组对象中查找最大值或最小值,使用堆能够高效率的完成需求。
排序算法中的堆排序正是利用了堆这一数据完成的排序,堆在实际应用中主要被用于实现优先队列(priority queue)下面我们以小顶堆为例学习一下堆的结构和常规操作。
堆的特性
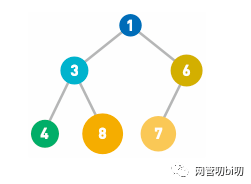
如上图所示,就是一个小顶堆,我们先来说说它的特性。
完全二叉树
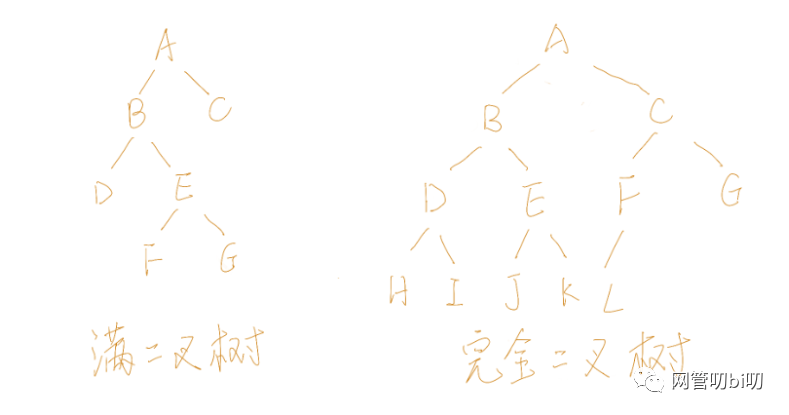
首先堆是一棵完全二叉树,关于完全二叉树和满二叉树:
如果一个二叉树的任何节点,要么是叶子节点,要么左右子树均非空,则这棵二叉树称做满二叉树(full binary tree)
如果一个二叉树最多只有最下面的两层节点度数可以小于2,并且最下面一层的节点都集中在该层最左边的连续位置上,则此二叉树称做完全二叉树(complete binary tree)
节点的规则
在小顶堆中存储数据时必须遵守这样一条规则 :堆中所有节点的值均不大于其左右子节点的值,一个节点与其兄弟节点之间没有必然的联系。
而在二叉查找树中是,左子 < 父 < 右子
存储结构
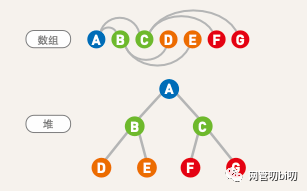
由于堆是一棵完全二叉树,可以用数组来存储,只需要通过简单的代数表达式,就能计算出要某个节点的父节点和子节点的索引位置,既避免了像链表那样使用指针来保持结构,又能高效的执行相应操作。关于节点的父节点和子节点在堆中的位置需要记住下面三个公式:
-
节点 i 的左子节点为2 * i + 1,右子节点为 2 * i+2 -
节点 i 的父节点为 (i - 1) /2
用Go实现堆操作
上面我们分析完堆的特性和存储结构后,我们自己用 Go 语言实现一个堆以及堆的各种操作。
数据结构
type Heap []int
// 交换两个节点的值
func (h Heap) swap(i, j int) {
h[i], h[j] = h[j], h[i]
}
// 比较两个节点的值
func (h Heap) less(i, j int) bool {
// 如果实现的是大顶堆,修改这里的判断即可
return h[i] < h[j]
}
上面我们定义了小顶堆的数据结构以及它的两个基本操作,比较以及交换两个节点的值。下面来实现堆结构上的常规操作。
插入
向堆中插入数据时,首先会把元素放到末尾。如下图所示,向小顶堆中插入一个值为 5 的节点
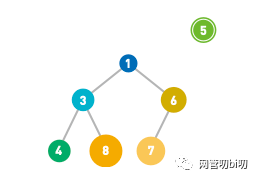
先把节点放到了堆的末尾
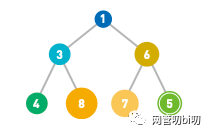
末尾插入新节点后,不再满足小顶堆的要求,故需要沿着其路径,自下而上依次比较和交换该节点与父节点的位置,直到重新满足小顶堆的性质为止。
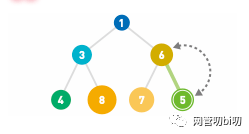
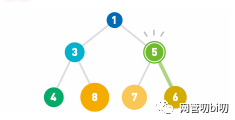
如上图所示,首先,新添加的节点加入到末尾。为了保持小顶堆的性质,需要让该节点沿着其路径,自下而上依次比较和交换自身与父节点点的位置,直到重新满足小顶堆的性质为止。
这样会出现两种情况,要么新节点一直升到堆顶,要么到某一位置时发现父节点比自己小,则停止。
上面的流程代码如下:
func (h Heap) up(i int) {
for {
f := (i - 1) / 2 // 父节点在数组中的位置
if i == f || h.less(f, i) {
break
}
h.swap(f, i)
i = f
}
}
// 注意go中所有参数都是值传递
// 所以要让h的变化在函数外也起作用,此处要传指针
func (h *Heap) Push(x int) {
*h = append(*h, x)
h.up(len(*h) - 1)
}
删除
从最小堆中删除节点,分为以下三个步骤
-
把最末端的节点和要删除节点的位置进行交换。 -
删除末端节点 -
原来的末端节点需要与新位置上的父节点做比较,如果小于要做 up(看上面的方法),如果大于父节点,则再和子节点做比较,即 down 操作,直到该节点下降到小于最小子节点为止。
与子节点进行比较交换的 down 操作的流程用代码表示为:
func (h Heap) down(i int) {
for {
l := 2*i + 1 // 左孩子
r := 2*i +2 // 右孩子
if l >= len(h) {
break // i 已经是叶子节点,退出操作。
}
j := l
if r < len(h) && h.less(r, l) {
j = r // 右孩子为最小子节点
}
// i 与最小子节点进行比较
if h.less(i, j) {
break // 如果父节点比子节点小,则不交换
}
h.swap(i, j) // 交换父子节点
i = j //继续向下比较
}
}
实现了核心的up 和down 操作后,堆的Remove操作便很简单,代码如下:
// 删除堆中位置为i的元素
// 返回被删元素的值
func (h *Heap) Remove(i int) (int, bool) {
if i < 0 || i > len(*h)-1 {
return 0, false
}
n := len(*h) - 1
h.swap(i, n) // 用最后的元素值替换被删除元素
// 删除最后的元素
x := (*h)[n]
*h = (*h)[0:n]
// 如果当前元素大于父节点,向下筛选
if i == 0 || (*h)[i] > (*h)[(i-1)/2] {
h.down(i)
} else { // 当前元素小于父节点,向上筛选
h.up(i)
}
return x, true
}
弹出堆顶元素
弹出堆顶元素,就是删除 i = 0 的节点。
// 弹出堆顶的元素,并返回其值
func (h *Heap) Pop() int {
x, _ := h.Remove(0)
return x
}
建堆
讲完了堆的核心操作 up 和 down 后,我们来看一下如何根据一个数组构造一个小顶堆。
建立堆的过程就是完全二叉树,从下到上调整堆的过程,从 i = len(arr) /2 开始依次向上调整,i = len(arr) /2是堆中末尾节点的父节点, i=0是根节点。
func BuildHeap(arr []int) Heap {
h := Heap(arr)
n := len(h)
// 从第一个非叶子节点,到根节点
for i := n/2 - 1; i >= 0; i-- {
h.down(i)
}
return h
}堆排序
学完堆的基础知识后,我们再来看堆排序就变得非常简单。利用最小堆的特性,我们每次都从堆顶弹出一个元素(这个元素就是当前堆中的最小值),即可实现升序排序。代码如下:
func HeapSort(arr []int) {
// 创建堆
heap := BuildHeap(arr)
var sortedArr []int
for len(heap) > 0 {
sortedArr = append(sortedArr, heap.Pop())
}
fmt.Println(sortedArr)
}
func main() {
//输出 [3 8 10 15 15 16 17 19 24 30 33]
HeapSort([]int{33, 24, 8, 3, 10, 15, 16, 15, 30, 17, 19})
}
Go标准库对堆的定义
堆是一种很好的实现优先队列的数据结构,我们在这里自己实现了一个小顶堆。Go 在它的标准库 container/heap 也提供了堆的定义,
type Interface interface {
sort.Interface
Push(x any) // add x as element Len()
Pop() any // remove and return element Len() - 1.
}
它匿名嵌套的 sort.Interface 的定义如下:
type Interface interface {
// Len is the number of elements in the collection.
Len() int
// Less reports whether the element with
// index i should sort before the element with index j.
Less(i, j int) bool
// Swap swaps the elements with indexes i and j.
Swap(i, j int)
}
也就是说,我们要使用go标准库给我们提供的heap,那么必须自己实现上面两个接口定义的方法,这些方法的实现方式就是我们上面演示的建堆、插入、删除这些操作,这里就不再继续演示 Go 这个 heap 库的使用啦。
参考
-
图例来自《我的第一本算法书》 -
https://www.cnblogs.com/yahuian/p/go-heap.html